红黑树

January 11, 2022

树，保持高效在于平衡，高度低。

红黑树如何做到的呢？

定义 #

wiki #

红黑树（英语：Red–black tree）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型用途是实现关联数组。它在1972年由鲁道夫·贝尔发明，被称为"对称二叉B树"，它现代的名字源于Leo J. Guibas和罗伯特·塞奇威克于1978年写的一篇论文。红黑树的结构复杂，但它的操作有着良好的最坏情况运行时间，并且在实践中高效：它可以在O(log n)时间内完成查找、插入和删除，这里的n是树中元素的数目。

性质 #

红黑树是每个节点都带有颜色属性的二叉查找树，颜色为红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求：

节点是红色或黑色。
根是黑色。
所有叶子都是黑色（叶子是NIL节点）。
每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）
从**任一节点到其每个叶子**的所有简单路径都包含**相同数目的黑色节点**。

一句话概况：或红或黑，首尾皆黑，红子必黑，任一点至所有尾含黑同数。

为确保任一点至所有尾含黑同数，路径中必须插入红点，而在哪个位置插呢（必须考虑红子必黑原则）？

这些约束确保了红黑树的关键特性：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。
要知道为什么这些性质确保了这个结果，注意到性质4导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点，最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点，这就表明了没有路径能多于任何其他路径的两倍长。
在很多树数据结构的表示中，一个节点有可能只有一个子节点，而叶子节点包含数据。用这种范例表示红黑树是可能的，但是这会改变一些性质并使算法复杂。为此，本文中我们使用"nil叶子"或"空（null）叶子"，如上图所示，它不包含数据而只充当树在此结束的指示。这些节点在绘图中经常被省略，导致了这些树好像同上述原则相矛盾，而实际上不是这样。与此有关的结论是所有节点都有两个子节点，尽管其中的一个或两个可能是空叶子。

实现 #

操作 #

因为每一个红黑树也是一个特化的二叉查找树，因此红黑树上的只读操作与普通二叉查找树上的只读操作相同。然而，在红黑树上进行插入操作和删除操作会导致不再符合红黑树的性质。恢复红黑树的性质需要少量（O(log n)）的颜色变更（实际是非常快速的）和不超过三次树旋转（对于插入操作是两次）。虽然插入和删除很复杂，但操作时间仍可以保持为O(log n)次。

我们首先以二叉查找树的方法增加节点并标记它为红色。（如果设为黑色，就会导致根到叶子的路径上有一条路上，多一个额外的黑节点，这个是很难调整的。但是设为红色节点后，可能会导致出现两个连续红色节点的冲突，那么可以通过**颜色调换（color flips）和树旋转**来调整。）

树旋转 #

对二叉树的一种操作，不影响元素的顺序，但会改变树的结构，将一个节点上移、一个节点下移。树旋转会改变树的形状，因此常被用来将较小的子树下移、较大的子树上移，从而降低树的高度、提升许多树操作的效率。

树旋转

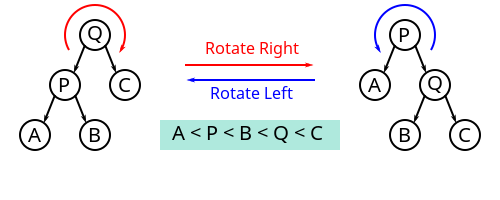
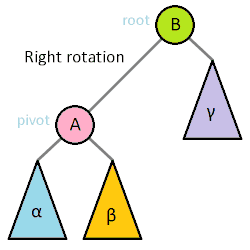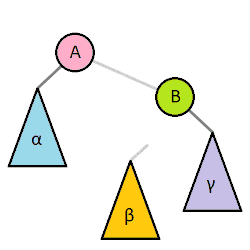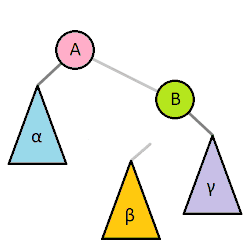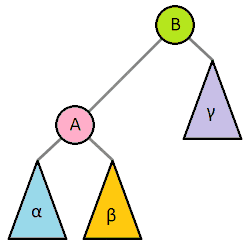
树旋转动图

对一棵树进行旋转时，这棵树的根节点是被旋转的两棵子树的父节点，称为旋转时的根（英语：root）；如果节点在旋转后会成为新的父节点，则该节点为旋转时的转轴（英语：pivot）。

上图中，树的右旋操作以 Q 为根、P 为转轴，会将树顺时针旋转。相应的逆操作为左旋，会以 Q 为转轴，将树逆时针旋转。

理解树旋转过程的关键，在于理解其中不变的约束。旋转操作不会导致叶节点顺序的改变（可以理解为旋转操作前后，树的中序遍历结果是一致的），旋转过程中也始终受二叉搜索树的主要性质约束：右子节点比父节点大、左子节点比父节点小。尤其需要注意的是，进行右旋转时，旋转前根的左节点的右节点（例如上图中以 Q 为根的 B 节点）会变成根的左节点，根本身则在旋转后会变成新的根的右节点，而在这一过程中，整棵树一直遵守着前面提到的几个约束。相反的左旋转操作亦然。

如果将根记为 Root、转轴记为 Pivot、子节点中与旋转方向相同的一侧记为 RS（旋转侧，英语：Rotation Side）、旋转对侧记为 OS（英语：Opposite Side），则上图中 Q 节点的 RS 为 C、OS 为 P，将其右旋转的伪代码为：

Pivot = Root.OS
Root.OS = Pivot.RS
Pivot.RS = Root
Root = Pivot

该操作为常数时间复杂度。

代码 #

package redblacktree

import "fmt"

type Color int

const (
	Red   Color = 0
	Black Color = 1
)

func (color Color) output() string {
	switch color {
	case Red:
		return "RED"
	case Black:
		return "BLACK"
	default:
		return ""
	}
}

type Node struct {
	value int
	color Color

	leftTree, rightTree, parent *Node
}

// Grandparent 爷
func (node *Node) Grandparent() *Node {
	if node.parent == nil {
		return nil
	}
	return node.parent.parent
}

// Uncle 叔伯
func (node *Node) Uncle() *Node {
	if node.Grandparent() == nil {
		return nil
	}
	if node.parent == node.Grandparent().rightTree {
		return node.Grandparent().leftTree
	} else {
		return node.Grandparent().rightTree
	}
}

// Sibling 兄弟
func (node *Node) Sibling() *Node {
	if node.parent == nil {
		return nil
	}
	if node.parent.leftTree == node {
		return node.parent.rightTree
	} else {
		return node.parent.leftTree
	}
}

type RBT struct {
	root, NIL *Node
}

// 右翻转
// 涉及节点：本节点、父节点的左子节点、右节点、根节点、爷节点
// 移动方向：
func (t *RBT) rotateRight(node *Node) {
	gp := node.Grandparent()
	fa := node.parent
	rt := node.rightTree

	fa.leftTree = rt

	if rt != t.NIL {
		rt.parent = fa
	}
	node.rightTree = fa
	fa.parent = node

	if t.root == fa {
		t.root = rt
	}
	node.parent = gp

	if gp != nil {
		if gp.leftTree == fa {
			gp.leftTree = node
		} else {
			gp.rightTree = node
		}
	}
}

func (t *RBT) rotateLeft(node *Node) {
	if node.parent == nil {
		t.root = node
		return
	}
	gp := node.Grandparent()
	fa := node.parent
	lt := node.leftTree

	fa.rightTree = lt

	if lt != t.NIL {
		lt.parent = fa
	}
	node.leftTree = fa
	fa.parent = node

	if t.root == fa {
		t.root = node
	}
	node.parent = gp

	if gp != nil {
		if gp.leftTree == fa {
			gp.leftTree = node
		} else {
			gp.rightTree = node
		}
	}
}

func (t *RBT) inorder(node *Node, level int) {
	level++
	var prefix string
	for i := 1; i < level; i++ {
		prefix += "  "
	}

	if node == t.NIL {
		fmt.Printf("%s-NIL(%s)\n", prefix, node.color.output())
		return
	}
	if node.leftTree != nil {
		t.inorder(node.leftTree, level)
	}

	fmt.Printf("%s-%d(%s)\n", prefix, node.value, node.color.output())

	if node.rightTree != nil {
		t.inorder(node.rightTree, level)
	}
}

func (t *RBT) getSmallestChild(node *Node) *Node {
	if node.leftTree == t.NIL {
		return node
	}
	return t.getSmallestChild(node.leftTree)
}

func (t *RBT) GetMaxChild(node *Node) *Node {
	if node.rightTree == nil {
		return node
	}
	return t.GetMaxChild(node.rightTree)
}

func (t *RBT) deleteChild(node *Node, data int) bool {
	if node.value > data {
		if node.leftTree == t.NIL {
			return false
		}
		return t.deleteChild(node.leftTree, data)
	} else if node.value < data {
		if node.rightTree == t.NIL {
			return false
		}
		return t.deleteChild(node.rightTree, data)
	} else if node.value == data {
		if node.rightTree == t.NIL {
			t.deleteOneChild(node)
			return true
		}

		smallest := t.getSmallestChild(node.rightTree)
		// swap(p->value, smallest->value)
		node.value, smallest.value = smallest.value, node.value
		t.deleteOneChild(smallest)

		return true
	}
	return false
}

func (t *RBT) deleteOneChild(node *Node) {
	var child *Node
	if node.leftTree == t.NIL {
		child = node.rightTree
	} else {
		child = node.leftTree
	}

	if node.parent == nil && node.leftTree == t.NIL && node.rightTree == t.NIL {
		node = nil
		t.root = node
		return
	}

	if node.parent == nil {
		child.parent = nil
		t.root = child
		t.root.color = Black
		return
	}

	if node.parent.leftTree == node {
		node.parent.leftTree = child
	} else {
		node.parent.rightTree = child
	}
	child.parent = node.parent

	if node.color == Black {
		if child.color == Red {
			child.color = Black
		} else {
			t.deleteCase(child)
		}
	}
}

func (t *RBT) deleteCase(node *Node) {
	if node.parent == nil {
		node.color = Black
		return
	}

	if node.Sibling().color == Red {
		node.parent.color = Red
		node.Sibling().color = Black
		if node == node.parent.leftTree {
			t.rotateLeft(node.parent)
		} else {
			t.rotateRight(node.parent)
		}
	}

	if node.parent.color == Black && node.Sibling().color == Black &&
		node.Sibling().leftTree.color == Black &&
		node.Sibling().rightTree.color == Black {
		node.Sibling().color = Red
		t.deleteCase(node.parent)
	} else if node.parent.color == Red &&
		node.Sibling().color == Black &&
		node.Sibling().leftTree.color == Black &&
		node.Sibling().rightTree.color == Black {
		node.Sibling().color = Red
		node.parent.color = Black
	} else {
		if node.Sibling().color == Black {
			if node == node.parent.leftTree &&
				node.Sibling().leftTree.color == Red &&
				node.Sibling().rightTree.color == Black {
				node.Sibling().color = Red
				node.Sibling().leftTree.color = Black
				t.rotateRight(node.Sibling().leftTree)
			} else if node == node.parent.rightTree &&
				node.Sibling().leftTree.color == Black &&
				node.Sibling().rightTree.color == Red {
				node.Sibling().color = Red
				node.Sibling().rightTree.color = Black
				t.rotateLeft(node.Sibling().rightTree)
			}
		}
		node.Sibling().color = node.parent.color
		node.parent.color = Black
		if node == node.parent.leftTree {
			node.Sibling().rightTree.color = Black
			t.rotateLeft(node.Sibling())
		} else {
			node.Sibling().leftTree.color = Black
			t.rotateRight(node.Sibling())
		}
	}
}

func (t *RBT) insert(node *Node, data int) {
	if node.value >= data {
		if node.leftTree != nil && node.leftTree != t.NIL {
			t.insert(node.leftTree, data)
		} else {
			tmp := new(Node)
			tmp.value = data
			tmp.leftTree = t.NIL
			tmp.rightTree = t.NIL
			tmp.parent = node
			node.leftTree = tmp
			t.insertCase(tmp)
		}
	} else {
		if node.rightTree != nil && node.rightTree != t.NIL {
			t.insert(node.rightTree, data)
		} else {
			tmp := new(Node)
			tmp.value = data
			tmp.leftTree = t.NIL
			tmp.rightTree = t.NIL
			tmp.parent = node
			node.rightTree = tmp
			t.insertCase(tmp)
		}
	}
}

func (t *RBT) insertCase(node *Node) {
	if node.parent == nil {
		t.root = node
		node.color = Black
		return
	}
	fmt.Printf("insertCase: node: %+v, parent: %+v\n", node, node.parent)
	// t.inorder(t.root)
	if node.parent.color == Red {
		if node.Uncle() != nil && node.Uncle().color == Red {
			node.parent.color = Black
			node.Uncle().color = Black
			node.Grandparent().color = Red
			t.insertCase(node.Grandparent())
		} else {
			if node.parent.rightTree == node &&
				node.Grandparent().leftTree == node.parent {
				t.rotateLeft(node)
				node.color = Black
				node.parent.color = Red
				t.rotateRight(node)
			} else if node.parent.leftTree == node &&
				node.Grandparent().rightTree == node.parent {
				t.rotateRight(node)
				node.color = Black
				node.parent.color = Red
				t.rotateLeft(node)
			} else if node.parent.leftTree == node &&
				node.Grandparent().leftTree == node.parent {
				node.parent.color = Black
				node.Grandparent().color = Red
				t.rotateRight(node.parent)
			} else if node.parent.rightTree == node &&
				node.Grandparent().rightTree == node.parent {
				node.parent.color = Black
				node.Grandparent().color = Red
				t.rotateLeft(node.parent)
			}
		}
	}
}

func (t *RBT) DeleteTree(node *Node) {
	if node == nil || node == t.NIL {
		return
	}
	t.DeleteTree(node.leftTree)
	t.DeleteTree(node.rightTree)
}

func (t *RBT) search(node *Node, data int) *Node {
	if node == nil {
		return nil
	}
	if node.value > data {
		if node.leftTree == nil {
			return nil
		}
		return t.search(node.leftTree, data)
	} else if node.value < data {
		if node.rightTree == nil {
			return nil
		}
		return t.search(node.rightTree, data)
	} else {
		return node
	}
}

func (t *RBT) Inorder() {
	if t.root == nil {
		return
	}
	t.inorder(t.root, 0)
	fmt.Println("")
}

func (t *RBT) Search(data int) (*Node, bool) {
	if t.root == nil {
		return nil, false
	}
	node := t.search(t.root, data)
	return node, node != nil
}

func (t *RBT) Insert(data int) {
	if t.root == nil {
		t.root = new(Node)
		t.root.color = Black
		t.root.leftTree = t.NIL
		t.root.rightTree = t.NIL
		t.root.value = data
	} else {
		t.insert(t.root, data)
	}
}

func (t *RBT) Delete(data int) bool {
	return t.deleteChild(t.root, data)
}

func NewRBT() *RBT {
	return &RBT{
		root: nil,
		NIL:  &Node{color: Black},
	}
}

分析 #

树皆有根，根连干，干连枝，枝连叶，盘根错节。通过红黑树的形式来管理这颗树，让树的营养均衡，从而保持长久的生命力。

命运扭成一个死结，怎么办？不如分散为独立事件，各自处理。分合之间，分久必合，合久必分。集权者只顾为己争权夺利，越集中越凶险，故分；诸侯王枉顾生死不辩是非互相倾轧，越分散越苦痛，故合。是合，是分，由谁定呢？什么时候定呢？感觉（分久必合，合久必分）这句话更多是作者的一种感慨，中间有太多无奈和哀伤。

达成共识，才能动工。社会是这样，皆因大部分人都认可这样。要想改变，从观念开始。只有达成新的共识，才能改变。至少要让有能力动手的达成共识。

如果都在一棵树上，树倒猢狲散，那么大家都会极力促成共识的达成吧。不过现实往往不只一颗树，并且每棵树还各自不一样，所以要想达成共识非常困难。如果各自有意愿往共识达成努力，也还能多交流、沟通，以图共识。万一各怀异心，就无法一致了。此时，付出更多的一方反而受伤越多、损失越重。